Question

Matrices C and D are shown below C= 2 1 0 0 3 4 0 2 1 D= a b -0.4 0 -0.2 0.8 0 0.4 -0.6 what values of a and b will make the equation CD = l true?

Answer 1

The question is incomplete. Here is the complete question

Matrices C and D are shown below:

`C=\left[\begin{array}{ccc}2&1&0\\0&3&4\\0&2&1\end{array}\right]`
`D=\left[\begin{array}{ccc}a&b&-0.4\\0&-0.2&0.8\\0&0.4&-0.6\end{array}\right]`

What values of a and b will make the equation CD = I true?

(i) a = 0.5

b = 0.1

(ii) a = 0.1

b = 0.5

(iii) a = -0.5

b = -0.1

Answer: (i) a = 0.5

b = 0.1

Explanation: Identity Matrix (I) is a n x n square matrix with the number 1 on the main diagonal and 0 everywhere else.

The question asks for multiplication of matrices, i.e.:

`\left[\begin{array}{ccc}2&1&0\\0&3&4\\0&2&1\end{array}\right]` .
`\left[\begin{array}{ccc}a&b&-0.4\\0&-0.2&0.8\\0&0.4&-0.6\end{array}\right]` =
`\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right]`

To multiply matrices, the number of columns of the 1st matrix must be the same as the number of rows of the 2nd.

Matrix C is a 3x3 square matrix and so is matrix D, so, values of a and b:

`2a=1`
`2b-0.2=0`

`a=(1)/(2)`
`2b=0.2`

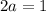
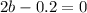
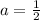
a = 0.5
`b=0.1`

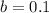
For the equation CD=I be true, a and b has to be 0.5 and 0.1, respectively.