Question

Please help me on this

Answer 1

Answer: option a.

Explanation:

Given the expression
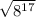`\sqrt{8^(17)}`, you need to remember:

The Product of powers property:

`a^m*a^n=a^((m+n))`

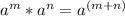
The Power of a power property:

`(a^m)^n=a^(mn)`

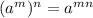
And:

`\sqrt[n]{a^n}=a`

Therefore, as the index of the radical is 2, you can rewrite
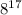`8^(17)` as:

`8^(17)=8^(16)*8`

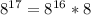
Rewrite this and simplify. Then:

`=\sqrt{8^(17)}`

`=\sqrt{8^(16)*8}=\sqrt{8^(16)}√(8)=\sqrt{(8^(8))^2}√(8)=8^8√(8)`

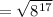
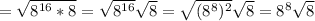
This matches with the option a.