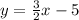Question

Mia drew a map of a park. Mia’s map shows the endpoints of the walking paths at A(2, 2), B(2, 6), C(8, 6), and D(8, 2). There are 6 walking paths: AB, BC, CD, AD, AC, and BD.

1. Are walking paths AB and CD parallel? Explain.

2. Are walking paths AC and BD perpendicular? Explain.

3. Mia also drew path FG that goes through (12, 2) on her map and is parallel to path AC. Write an equation for path FG.

4. Mia also drew path MN that goes through (10, 10) on her map and is perpendicular to path BD. Write an equation for path MN.

Answer 1

1. yes, because they both have the same undefinite slopes. They are both vertical lines.

2. no, because their slopes are not negative reciprocals.

3.
`y=(2)/(3)x-6`

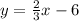
4.
`y=(3)/(2)x+5`

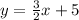
Explanation:

In order to solve this problem, we can start by drawing a diagram of the paths Mia drew. (See attached picture the red lines are the original paths).

1. In order to determine if the paths are parallel or not, we need to first know what the slope of the paths is. The slope of the paths can be found by using the equation:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

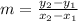
So, for path AB we get:

`m_(AB)=(6-2)/(2-2)`

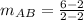
which yields:

`m_(AB)=(4)/(0)`

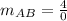
Now, since we have a denominator of 0 in that friction, this means that the division is not defined for the real number, therefore, we are dealing with a vertical line.

for the path CD we get:

`m_(CD)=(2-6)/(8-8)`

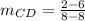
which yields:

`m_(AB)=-(4)/(0)`

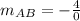
Now, since we have a denominator of 0 in that friction, this means that the division is not defined for the real number, therefore, we are dealing with a vertical line.

Therefore, since both slopes are the same, this means that the two lines will be parallel.

2. The procedure is the same as in the previous problem:

`m_(AC)=(6-2)/(8-2)`

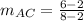
which yields:

`m_(AC)=(2)/(3)`

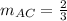
for the path BD we get:

`m_(BD)=(2-6)/(8-2)`

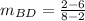
which yields:

`m_(BD)=-(2)/(3)`

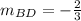
This two fractions are just opposite in sign. But for the lines to be perpendicular, their slopes should be negative reciprocal. In this case they are not reciprocal, so the lines are not perpendicular to each other.

3. For part 3, we know that for two lines to be parallel, their slopes must be the same. We already found the slope of AC to be:

`m_(AC)=(2)/(3)`

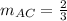
we also know the line must go through the point (12,2), so we can use the point-slope form of the equation:

`y-y_(1)=m(x-x_(1))`

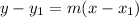
so we can go ahead and substitute the pertinent data:

`y-2=(2)/(3)(x-12)`

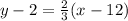
So now we can solve it for y so it gets the slope-intercept form, which is:

`y=(2)/(3)x-6`

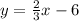
4. In this part of the problem, we will need to follow a similar process, but this time, we need the slope to be negative reciprocal to slope of the line BD.

`m_(BD)=-(2)/(3)`

so:

`m_(MN)=(3)/(2)`

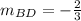
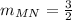
so now we can build our equation with the point-intercept form and the given point so we get:

`y-10=(3)/(2)(x-10)`

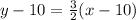
So now we can solve it for y so it gets the slope-intercept form, which is:

`y=(3)/(2)x-5`