Answer:
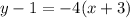
Explanation:
Given: A line has a slope of -4 and the line passes through a point
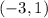 .
.
To find: The point-slope form of this line.
Solution:
We know, the point-slope form of a line can be given as

Here,
 is the slope of the line, and
is the slope of the line, and
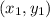 is the point through which it passes.
is the point through which it passes.
The slope of the line is -4, and the point is
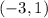 .
.
So,
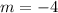 ,
,
 , and
, and
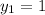 .
.
Now, putting the values in the equation, we get
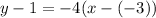
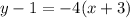
Therefore, the point-slope form of the line is
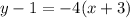 .
.