Answer:
A) 19 cm3
Explanation:
Volume of a cone is calculated as:
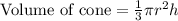
Volume of a cylinder is calculated as:
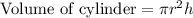
From the above two expressions we can see that if the height and radius of a cone and cylinder will be equal, the volume of cone will be 1/3 of the volume of the cylinder.
We are given the volume of Cylinder A to be 18π. So the volume of Cone B will be:
Volume of Cone B = 1/3 of Volume of Cylinder A
Volume of cone B = 1/3 x 18π = 6π = 19 cm³ (rounded to nearest whole number)
Thus, the volume of given cone B will be 19 cm³ rounded of to nearest whole number.