ANSWER
C) 1, 3, 6, 10, 15, 21, 28, 36, 45
Step-by-step explanation
The recursive formula is,

when n is a natural number greater than 1.
When n=2,
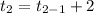
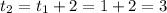
when n=3,

when t=4,
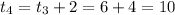
When t=5,

when t=6,.

when t=7
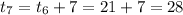
When t=8,
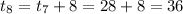
When t=9,
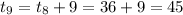
Hence the first nine triangular number are
C) 1, 3, 6, 10, 15, 21, 28, 36, 45