Question

Cone A has a radius of 2 inches and a height of 3 inches. In cone B, the height is the same, but the radius is doubled. Calculate the volume of both cones. Which statement is accurate? A) When the radius is doubled, the resulting volume is half that of the original cone. B) When the radius is doubled, the resulting volume is twice that of the original cone. Eliminate C) When the radius is doubled, the resulting volume is 4 times that of the original cone. D) When the radius is doubled, the resulting volume is 3 times that of the original cone.

Answer 1

C) When the radius is doubled, the resulting volume is 4 times that of the original cone

Explanation:

Volume of a cone is given by:

`Volume=(1)/(3) \pi r^(2)h`

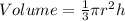
Cone A has radius = r = 2 inches and height = h = 3 inches

So, the volume of cone A will be:

`Volume=(1)/(3) \pi (2)^(2) * 3 = 4 \pi`

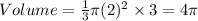
Height of cone B is same as cone A, so height of cone B = h = 3 inches

Radius of cone B is double of cone A, so radius of cone B = r = 4 inches

So, the volume of cone B will be:

`Volume=(1)/(3) \pi (4)^(2) * 3 = 16 \pi`

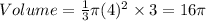
From here we can see that volume of cone B is 4 times the volume of cone A. Thus, doubling the radius increases the volume to 4 times.

So, option C is correct. When the radius is doubled, the resulting volume is 4 times that of the original cone

Answer 2

Answer: Option C.

Explanation:

Use the formula for calculate the volume of a cone:

`V=(1)/(3)\pi r^2h`

Where r is the radius and h is the height.

Volume of the cone A:

`V_A=(1)/(3)\pi (2in)^2(3in)=12.56in^3`

Volume of the cone B:

If the height of the cone B and the height of the cone A are the same , but the radius of the cone B is doubled, then its radius is:

`r_B=2r_A\\r_B=2*2in\\r_B=4in`

Then:

`V_B=(1)/(3)\pi (4in)^2(3in)=50.26in^3`

Divide
`V_B` by
`V_A`:

`(V_B)/(V_A)=(50.26in^3)/(12.56in^3)=4`

Therefore: When the radius is doubled, the resulting volume is 4 times that of the original cone.