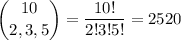There are
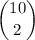 ways of picking 2 of the 10 available positions for a 0. 8 positions remain.
ways of picking 2 of the 10 available positions for a 0. 8 positions remain.
There are
 ways of picking 3 of the 8 available positions for a 1. 5 positions remain, but we're filling all of them with 2s, and there's
ways of picking 3 of the 8 available positions for a 1. 5 positions remain, but we're filling all of them with 2s, and there's
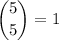 way of doing that.
way of doing that.
So we have
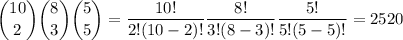
The last expression has a more compact form in terms of the so-called multinomial coefficient,