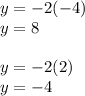Answer:
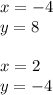
Explanation:
Make both equations equal to each other and solve for x:
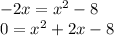
Factor the quadratic equation. You need to find two number that when you add them you get 2 and when you multiply them you get -8.
These numbers are 4 and -2. Then:
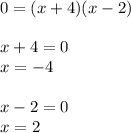
Substitute the values of x calculated, into any of the original equations. Then: