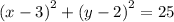Question

Write the equation of a circle in standard form with diameter stack A B with bar on top. Where A(7, 5) and B(-1, -1). For full credit, show your work.

Answer 1

`{(x - 3)}^(2) + {(y - 2)}^(2) = 25`

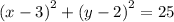
Step-by-step explanation

The given circle has diameter A(7,5) and B(-1,-1).

The center of the circle is the midpoint of the diameter.

The midpoint is given by the formula:

`((x_1+x_2)/(2) , (y_1+y_2)/(2) )`

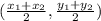
We substitute the points to get

`((7+ - 1)/(2) , (5+ - 1)/(2) )`

`(3 , 2 )`

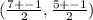
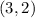
The radius of the circle is calculated using the center and any point on the circle.

`r = \sqrt{ {(x_2-x_1)}^(2) + {(y_2-y_1)}^(2) }`

`r = \sqrt{ {(3- - 1)}^(2) + {(2 - - 1)}^(2) }`

`r = √(16 + 9 )`

`r = √(25) = 5`

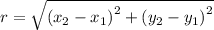
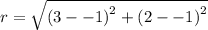
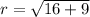
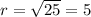
We substitute the center and the radius into the standard equation of the circle.

`{(x - h)}^(2) + {(y - k)}^(2) = {r}^(2)`

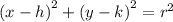
Substitute the values to get,

`{(x - 3)}^(2) + {(y - 2)}^(2) = {5}^(2)`

`{(x - 3)}^(2) + {(y - 2)}^(2) = 25`