Answer:
The test statistic 't' = 0.68 < 2.1314 at 0.05 level of significance
Null Hypothesis is accepted
There is no sufficient evidence to support the claim that the boards are either too long or too short
Explanation:
Step(i):-
Mean of the Population (μ) = 2857.0 millimetres
size of the sample 'n' = 16
Mean of the sample (x⁻) = 2858.7 millimetres
The Variance of the sample (S²)= 100.00
Standard deviation of the sample (S) = √100 =10
Degrees of freedom = n-1 =16-1 =15
Level of significance =0.05
Tabulated value =
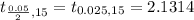
Step(ii):-
Null Hypothesis :H₀ : There is no sufficient evidence to support the claim that the boards are either too long or too short
Alternative Hypothesis: H₁:There is sufficient evidence to support the claim that the boards are either too long or too short
Test statistic
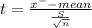
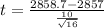
t = 0.68
The calculated value = 0.68 < 2.1314 at 0.05 level of significance
Null Hypothesis is accepted
Final answer:-
There is no sufficient evidence to support the claim that the boards are either too long or too short