Question

Which expression is equivalent to the given expression 10q+5

Answer 1

Hello!

The answers are:

`10q+5=5q+5q+5`

`10q+5=5(2q+1)`

`10q+5=10(q+(1)/(2))`

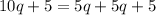
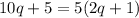
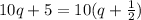
Why?

It's common to find more than just one equivalent expression to other expression since a number can be written in several ways and it will be the same.

The given expression is:

`10q+5`

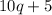
The given expression can be written like:

`10q+5=5q+5q+5`

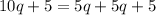
or

`10q+5=5(2q+1)`

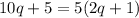
We can also write the expression using fractions!

`10q+5=10(q+(1)/(2))`

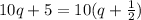
Have a nice day!