Question

51. If two cylinders of dissimilar geometry are connected together to form a closed hydrostatic system, why would one cylinder piston travel a greater distance than the other

Answer 1

see that for the same pressure the displaced height in each cylinder is different because its diameter is different. Pascal's principle

Step-by-step explanation:

The pressure on a system is given by the relations

P = ρ g h

P = F / A

where ρ is the density of the liquid, h the height and A the area

The expressions above we see that if for the same height the pressure is the same regardless of the shape of the cylinder.

With the second expression we see that if the system has a different area, the pressure is

P =
`(F_(1) )/(A_(1) ) = (F_(2) )/(A_(2) )`

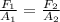
where we use subscript 1 for one body and subscript 2 for the other body

F₁ =
`(A_(1) )/(A_(2) ) F_(2)`

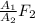
The cylinder displacement is

V = A h

where V is the volume and h the height, in general the liquids are incompressible therefore the displaced volume is constant in the two bodies

V = A₁ h₁ = A₂ h₂

`(A_(1) )/(A_2) = (h_2)/(h_1)`

we substitute

F₁ =
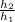`(h_2)/(h_1)` F2

From here we see that for the same pressure the displaced height in each cylinder is different because its diameter is different.

If the diameter is the same, the offset height is the same