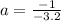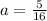Question

For what values of a is the value of the binomial 2a−1 smaller than the value of the binomial 7−1.2a by 7?

Answer 1

`a = (5)/(16)`

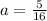
Step-by-step explanation

We want to find the value of a for which the binomial, 2a-1 is smaller than the value of the binomial 7-1.2a by 7.

This means that, when we subtract 2a-1 from 7-1.2a, we should get 7.

`7 - 1.2a - (2a - 1) = 7`

Expand:

`7 - 1.2a - 2a + 1= 7`

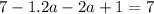
Group similar terms:

`- 1.2a - 2a = 7 - 7 - 1`

`- 3.2a = - 1`

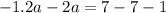
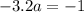
Divide both sides by -3.2,

`a = ( - 1)/( - 3.2)`

`a = (5)/(16)`