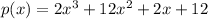A polynomial of degree 3 has exactly 3 solutions if we use complex numbers. If the polynomial has real coefficients and z is a complex solution, i.e.,
 , the conjugate is also a solution:
, the conjugate is also a solution:

So, in the first case, if we know that 1-i is a solution, the conjugate 1+i must be a solution as well.
So, we know all the roots: -5, 1+i, 1-i.
When you know the solutions
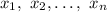 of a polynomial, you can write the polynomial (up to multiples) as
of a polynomial, you can write the polynomial (up to multiples) as
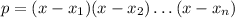
So, in your case, we have

You can check that indeed
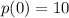 , because the constant term is 10, so, we're ok with this
, because the constant term is 10, so, we're ok with this
The second exercise is exactly the same: the solutions -6, i, -i identify the polynomial
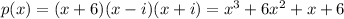
In this case, P(-3)=30, so if we want P(-3)=60 we have to multiply everything by 2: