Question

A certain forest covers an area of 4900km^2. Suppose that each year this area decreases by 7.25%. What will the area be after 5 years?

Use the calculator provided and round your answer to the nearest square kilometer

Answer 1

Each year, the forest decreases in area by 7.25%, which means that 92.75% of the forest remains each year.

With this, we can write a basic exponential decay equation:

4900*(0.9275)^t

Where t is the number of years past.

When you plug in 5 for t, the result shows that 3363.3005km^2 offorest will remain.

Hope this was helpful!

Answer 2

Answer:
`3,363.30km^2`

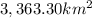
Explanation:

You need to use the following Exponential decay formula:

`y = P(1 - r)^t`

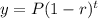
Where:

"P" is the initial amount, "r" is the rate in which the initial amount is decreasing and "t" is the period of time.

Then, you need to substitute values into the formula. You know that:

`P=4,900\\\\r=(7.25)/(100)\\\\t=5`

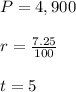
Therefore, by substituting these values into the formula, you get that the area of the forest after 5 years will be:

`y = 4,900(1 - (7.25)/(100) )^5\\y=3,363.30km^2`