Question

Brian is 6 feet tall and cast a 4 foot shadow. At the same time, a nearby flag pole cast a 20 foot shadow. How y’all is the pole?

Answer 1

scale factor=shadow: real figure

s.f=4:6

=2:3

applying the same to the pole

let x be the real height of the pole.

2:3=20/x

3×20=2x

60=2x

60/2=2x/2

x=30feet

Answer 2

30 ft.

Explanation:

We have been given that Brian is 6 feet tall and cast a 4 foot shadow. At the same time, a nearby flag pole cast a 20 foot shadow. We are asked to find height of the pole.

We will use proportions to solve our given problem.

`\frac{\text{Height of pole}}{\text{Shadow of pole}}=\frac{\text{Brian's height}}{\text{Brian's shadow}}`

`\frac{\text{Height of pole}}{\text{20 ft}}=\frac{\text{6 ft}}{\text{4 ft}}`

`\frac{\text{Height of pole}}{\text{20 ft}}*\text{20 ft}=\frac{\text{6 ft}}{\text{4 ft}}*\text{20 ft}`

`\text{Height of pole}=\frac{\text{6 ft}}{1}*5`

`\text{Height of pole}=\text{30 ft}`

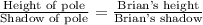
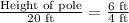
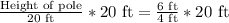
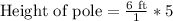
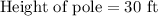
Therefore, the pole is 30 ft high.