Question

40 POINTS AVAILABLE

Given that A is the center of the concentric circles and BCDE is a square with AB = 18, find the area of the shaded region. Report your final answer(see picture below)

Answer 1

The area of the shaded region is
`(486\pi-648)\ units^(2)`

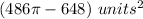
Explanation:

we know that

The area of the shaded region is equal to the area of the larger circle minus the area of the square plus the area of the smaller circle

Step 1

Find the area of the larger circle

The area of the circle is equal to

`A=\pi r^(2)`

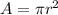
we have

`r=AB=18\ units`

substitute in the formula

`A=\pi (18)^(2)=324\pi\ units^(2)`

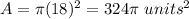
step 2

Find the length of each side of square BCDE

we have that

`AB=18\ units`

The diagonal DB is equal to

`DB=(2)18=36\ units`

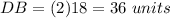
Let

x------> the length side of the square BCDE

Applying the Pythagoras Theorem

`36^(2)=x^(2) +x^(2)\\ 1,296=2x^(2)\\ 648=x^(2)\\ x=√(648)\ units`

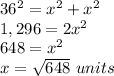
step 3

Find the area of the square BCDE

The area of the square is

`A=(√(648))^(2)=648\ units^(2)`

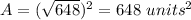
step 4

Find the area of the smaller circle

The area of the circle is equal to

`A=\pi r^(2)`

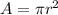
we have

`r=(√(648))/2\ units`

substitute in the formula

`A=\pi ((√(648))/2)^(2)=162\pi\ units^(2)`

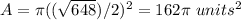
step 5

Find the area of the shaded region

`324\pi\ units^(2)-648\ units^(2)+162\pi\ units^(2)=(486\pi-648)\ units^(2)`