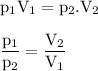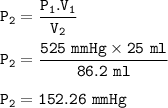The new pressure when the volume has been increased : 152.26 mmHg
Further explanation
Given
V₁ = 25 ml
P₁ = 525 Maggie ? (maybe you mean mmHg)
V₂ = 86.2 ml
Required
The new pressure
Solution
Boyle's Law
At a constant temperature, the gas volume is inversely proportional to the pressure applied