Question

Create a matrix for this system of linear equations, The determinant of the coefficient matrix is

Answer 1

Answer: The determinant of the coefficient matrix is -15 and x = 3, y = 4, z = 1.

Step-by-step explanation: The given system of linear equations is :

`2x+y+3z=13~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)\\\\x+2y=11~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(ii)\\\\3x+z=10~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(iii)`

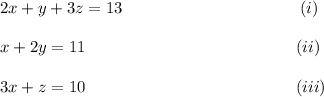
We are given to find the determinant of the coefficient matrix and to find the values of x, y and z.

The determinant of the co-efficient matrix is given by

`D=\begin{vmatrix}2 & 1 & 3\\ 1 & 2 & 0\\ 3 & 0 & 1\end{vmatrix}=2(2-0)+1(0-1)+3(0-6)=4-1-18=-15.`

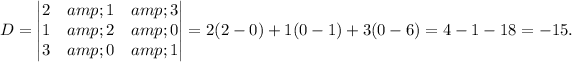
Now, from equations (ii) and (iii), we have

`x+2y=11~~~~~\Rightarrow y=(11-x)/(2)~~~~~~~~~~~~~~~~~~~~~~~~~~(iv)\\\\\\3x+z=10~~~~~~\Rightarrow z=10-3x~~~~~~~~~~~~~~~~~~~~~~~~~(v)`

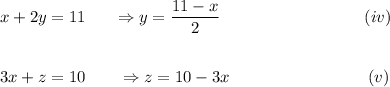
Substituting the value of y and z from equations (iv) and (v) in equation (i), we get

`2x+y+3z=13\\\\\Rightarrow 2x+(11-x)/(2)+3(10-3x)=13\\\\\Rightarrow 4x+11-x+60-18x=26\\\\\Rightarrow -15x+71=26\\\\\Rightarrow -15x=26-71\\\\\Rightarrow -15x=-45\\\\\Rightarrow x=3.`

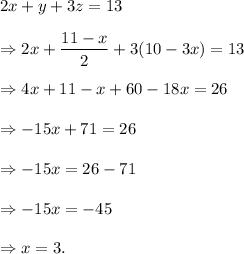
From equations (iv) and (v), we get

`y=(11-3)/(2)=4,\\\\z=10-3*3=1.`

Thus, the determinant of the coefficient matrix is -15 and x = 3, y = 4, z = 1.