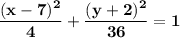\Answer:

Explanation:
Equation of The Ellipse
Given the center (h,k) and the length of the major and minor axis, we can write the equation of the ellipse as follows:
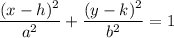
If the major axis is a, then the ellipse is horizontal, if the major axis is b, then the ellipse is vertical.
The ellipse shown in the figure is centered at (7,-2). The major axis is b and it can be found by measuring the distance from the center up or down to any vertex. We find b=6 and a=2.
Thus, the equation of the ellipse is:
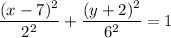
Operating: