Answer:
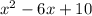
Explanation:
We know that the imaginary number i =
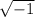 and thus
and thus
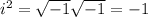
If roots are given in the form (a+bi) and (a-bi), to find the quadratic, we can write it in the form:
(x - (a+bi) ) * (x - (a-bi))
and then multiply to figure out the answer. Shown below:
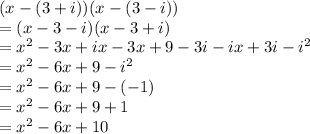
Thus, the BLANK is -6x