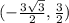QUESTION 1
We want to convert
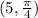 from polar coordinates to rectangular coordinates.
from polar coordinates to rectangular coordinates.
We use the formula;

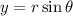
We plug in
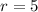 and
and
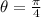 to obtain;
to obtain;
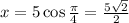
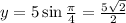
The rectangular coordinate is
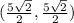
QUESTION 2
We want to convert
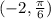 from polar coordinates to rectangular coordinates.
from polar coordinates to rectangular coordinates.
We use the formula;

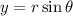
We plug in
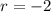 and
and
 to obtain;
to obtain;
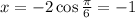
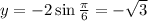
The rectangular coordinate is
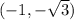
QUESTION 3
We want to convert
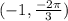 from polar coordinates to rectangular coordinates.
from polar coordinates to rectangular coordinates.
We use the formula;

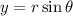
We plug in
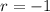 and
and
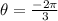 to obtain;
to obtain;
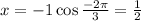
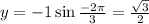
The rectangular coordinate is
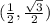
QUESTION 4
We want to convert
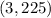 from polar coordinates to rectangular coordinates.
from polar coordinates to rectangular coordinates.
We use the formula;

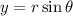
We plug in
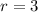 and
and
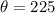 to obtain;
to obtain;
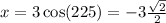
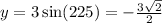
The rectangular coordinate is
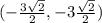
QUESTION 5
We want to convert
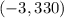 from polar coordinates to rectangular coordinates.
from polar coordinates to rectangular coordinates.
We use the formula;

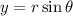
We plug in
 and
and
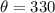 to obtain;
to obtain;
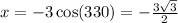

The rectangular coordinate is