Question

A biased dice is thrown.

Here are the probabilities of each score.
Score
1
2
3
4
5
6
Probability
0.15
0.05
0.25
0.05
0.3
0.2
The dice is thrown 300 times.
Work out the expected number of times the score will be odd.

Answer 1

Given:

A biased dice is thrown 300 times.

Table of probabilities of each score.

To find:

The expected number of times the score will be odd.

Solution:

Odd numbers on the dice are 1, 3, 5. The sum of their probability is

`0.15+0.25+0.3=0.7`

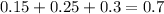
Even numbers on the dice are 2, 4, 6. The sum of their probability is

`0.05+0.05+0.2=0.3`

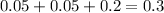
Now, the expected number of times the score will be odd is

`\text{Expected odd number}=300* \text{Probability of getting an odd number}`

`\text{Expected odd number}=300* 0.7`

`\text{Expected odd number}=210`

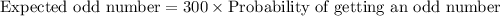
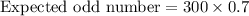
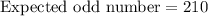
Therefore, the expected number of times the score will be odd is 210.