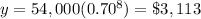Question

A delivery truck is purchased new for $54,000.

a. Write a linear function of the form y = mt + b to represent the value y of the vehicle t years after purchase. Assume that the vehicle is depreciated by $ 6750 per year.
b. Suppose that the vehicle is depreciated so that it holds 70% of its value form the previous year. Write an exponential function of the form y = Vobt where V0 is the initial value and t is the number of years after purchase.
c. To the nearest dollar, determine the value of the vehicle after 4 yr and after 8 yr using the linear model.
d. To the nearest dollar, determine the value of the vehicle after 4 yr and after 8 yr using the exponential model.

Answer 1

Part a)
`y=-6,750t+54,000`

Part b)
`y=54,000(0.70^(t))`

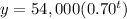
Part c) The value of the vehicle after 4 yr is $27,000 and the value of the vehicle after 8 yr is $0

Part d) The value of the vehicle after 4 yr is $12,965 and the value of the vehicle after 8 yr is $3,113

Explanation:

Part a) Write a linear function

Let

y -----> the value of the vehicle

t ----> the time in years after purchase

The equation in slope intercept form is equal to

`y=mt+b`

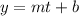
where

m is the slope

b is the y-intercept (original value)

we have

`m=-6,750(\$)/(year)`

`b=\$54,000`

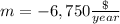
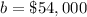
substitute

`y=-6,750t+54,000`

Part b) write an exponential function of the form

`y=V0(b^(t))`

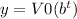
we have

`V0=\$54,000`

`b=70\%=70/100=0.70`

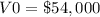
substitute

`y=54,000(0.70^(t))`

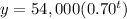
Part c) To the nearest dollar, determine the value of the vehicle after 4 yr and after 8 yr using the linear model

`y=-6,750t+54,000`

For t=4 year

substitute

`y=-6,750(4)+54,000=\$27,000`

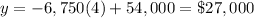
For t=8 year

substitute

`y=-6,750(8)+54,000=\$0`

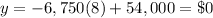
Part d) To the nearest dollar, determine the value of the vehicle after 4 yr and after 8 yr using the exponential model.

For t=4 year

substitute

`y=54,000(0.70^(4))=\$12,965`

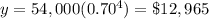
For t=8 year

substitute

`y=54,000(0.70^(8))=\$3,113`