Hello!
The answer is:
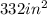
Why?
From the statement we know that the octagon has a apothem of 10in and a perimeter of 66.3in, and we are asked to find the area of the octagon.
We can use the following formula:
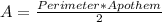
Substituting the given information into the area formula, we have:
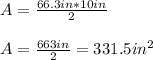
Rounding to the nearest number we have that:
331.5 ≈ 332
So, the area of the octagon is:
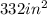
Have a nice day!