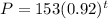Question

currently (2019), there are 153 bald eagles in Forest National Park. Bald eagles are an endangered species, and the population of bald eagles is decreasing by 8% every year. Write the equation that represents the population since 2019.

Answer 1

Answer:
`P=153(0.92)^t`

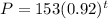
Explanation:

For this problem you need to use the formula for Exponential decay:

`P=P_0(1-r)^t`

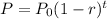
Where "
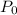`P_0`" is the initial population, "r" is the decay rate and "t" is the time in years.

With the information given, you can conclude that:

`t=0` represents the initial year (2019)

`P_0=153`

`r=(8)/(100)\\\\r=0.08`

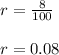
Finally, substituting these values into
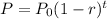`P=P_0(1-r)^t`, you get that the equation that represents the population since 2019 is:

`P=153(1-0.08)^t`

`P=153(0.92)^t`