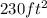Question

Carlos needs to paint the outside of the shed in his backyard, including its roof but not including its floor.

What is the total area of the surfaces that he needs to paint?

Answer 1

`230 ft^2`

Explanation:

Given : Carlos needs to paint the outside of the shed in his backyard, including its roof but not including its floor.

To Find: What is the total area of the surfaces that he needs to paint?

Solution:

Length of backyard= 8 feet

Breadth of backyard = 5 feet

Height of backyard = 6 feet

So, Area of walls of backyard = Lateral surface area =
`2(l+b) * h`

=
`2(8+5) * 6`

=
`156 ft^2`

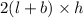
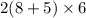
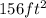
Area of two triangular faces of roof =
`(1)/(2) * Base * Height * 2`

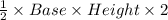
Base of triangular face = 8 feet

Height of triangular face = 3 feet

So, Area of two triangular faces of roof =
`(1)/(2) * 8 * 3 * 2`

=
`24 ft^2`

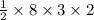
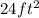
Area of two square roof =
`2 * Side^2`

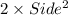
Side of square = 5 feet

So, Area of two square roof =
`2 * 5^2`

=
`50ft^2`

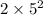
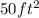
So, total area to be painted =
`156 ft^2+24 ft^2+50ft^2`

=
`230 ft^2`

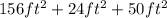
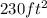
Hence the total area of the surfaces that he needs to paint is
`230 ft^2`

Answer 2

`230\ ft^(2)`

Explanation:

we know that

The total area of the surfaces that he needs to paint is equal to the lateral area of the rectangular prism plus the area of the two triangular faces and two square faces of the root.

so

`A=2(8+5)6+2[(1)/(2)(8)(3)]+2[5^(2)]\\ \\A=156+24+50\\ \\A=230\ ft^(2)`