Hello!
The graph is attached.
To graph a line, we first need to know:
- If the slope is increasing or decreasing
- Calculate the interception point with the axis
The slope of a line indicates if the function is increasing or decreasing.
We are given the function:

The slope is the coefficient of the variable (x), for this case, it's a positive value and it means that the function is increasing.
Calculating the interception points:
Let's make the function equal to 0 in order to find y-axis intercept:
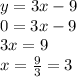
Then, substituting "x" into the function to find the y-axis interception point, we have:
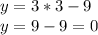
The first interception point is (3,0)
To find the second interception point, let's make "x" equal to 0:
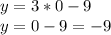
Then, substituting "y" into the function to find the x-axis interception point, we have:
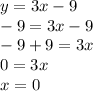
The second interception point is (0,-9)
Therefore,
We have a line which has a positive slope (increasing function) and intercepts the axis at (3,0) and (0,-9)
See the attached image for the graphic.
Have a nice day!