Question

use the determinant method to find the area of a triangle ABC with vertices at A (1,6) B (4,2) and C (-3,3)​

Answer 1

Area of triangle is 12.5

Explanation:

We need to use the determinant method to find the area of a triangle ABC with vertices at A (1,6) B (4,2) and C (-3,3)​

The formula used is:
`Area=\pm (1)/(2)\left|\begin{array}{ccc}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{array}\right|`

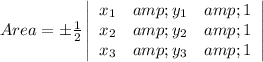
We are given:

`x_1=1,y_1=6,x_2=4,y_2=2,x_3=-3,y_3=3`

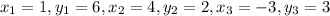
Putting values and finding area

`Area=(1)/(2)\left|\begin{array}{ccc}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{array}\right|\\Area=(1)/(2)\left|\begin{array}{ccc}1&6&1\\4&2&1\\-3&3&1\end{array}\right|\\Area=(1)/(2)(1\left|\begin{array}{cc}2&1\\3&1\end{array}\right|-6\left|\begin{array}{cc}4&1\\-3&1\end{array}\right|+1\left|\begin{array}{cc}4&2\\-3&3\end{array}\right| )\\Area=(1)/(2)(1(2-3)-6(4-(-3))+1(12-(-6)))\\Area= (1)/(2)(1(-1)-6(4+3)+1(12+6))\\Area= (1)/(2)(1(-1)-6(7)+1(18))\\Area= (1)/(2)(-1-42+18)\\`

`Area=(1)/(2)(-25)\\Area=-12.5\\`

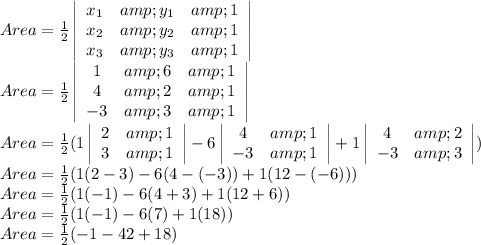
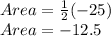
We take mode of -12.5 i.e. |-12.5| because area can't be negative.

`Now, \\Area=|-12.5|\\Area=12.5`

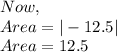
So, Area of triangle is 12.5