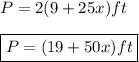Question

Help with this question, please!! I don't understand!!

Answer 1

`P=(19+50x)ft`

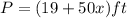
Explanation:

A rectangle is a quadrilateral whose angles are all right angles. In this problem, we have a rectangle whose height
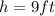`h=9ft` and whose area is
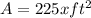`A=225xft^(2)`. We don't know the other side of the rectangle, but let's call it
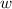`w`. So the area of a rectangle is:

`A=h.w`

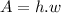
The perimeter is the distance around a shape in two dimensions. For our rectangle, our perimeter is:

`P=2h+2w`

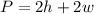
So our goal is to find
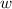`w`. From the equation of the area:

`w=(A)/(h) \\ \\ w=(225x)/(9)=25x`

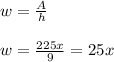
If we substitute both this value and the height in the equation of the perimeter we get:

`P=2(9+25x)ft \\ \\ \boxed{P=(19+50x)ft}`