Question

An electron moves to the left with a velocity of 9.6 x 10^5 m/s and has a magnetic force of 2.6 x 10^-15 N exerted on it. What is the magnitude of the magnetic field? Assume the charge has a value of 1.60 x 10^-19 C.

Answer 1

Magnetic field, B = 0.016 Tesla

Step-by-step explanation:

It is given that,

Velocity of electron,
`v=9.6* 10^5\ m/s`

Magnetic force,
`F=2.6* 10^(-15)\ N`

Charge,
`q=1.6* 10^(-19)\ N`

The magnetic force is given by :

`F=qvB`

`B=(F)/(qv)`

`B=(2.6* 10^(-15))/(1.6* 10^(-19)* 9.6* 10^5)`

`B=0.016\ T`

So, the magnitude of magnetic field is 0.016 Tesla. Hence, this is the required solution.

Answer 2

The magnitude of the magnetic field strength is 16.927 mT

Step-by-step explanation:

Given;

velocity of the electron, v = 9.6 x 10⁵ m/s

magnitude of the force exerted on the electron, F = 2.6 x 10⁻¹⁵ N

charge of electron, q = 1.60 x 10⁻¹⁹ C

The force exerted on the electron in magnetic field is given by charge times the vector product of velocity and magnetic field strength.

F = q(v x B)

where;

B is the magnetic field strength

`B = (F)/(qv)`

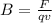
Substitute the given values of force, charge and velocity and calculate the magnetic field strength:

`B = (2.6*10^(-15))/((1.6*10^(-19))(9.6*10^5))} \\\\B = 1.6927*10^(-2) \ T\\\\B = 16.927 \ mT`

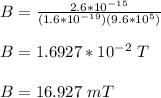
Therefore, the magnitude of the magnetic field strength is 16.927 mT