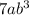Answer:
A)
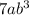
Explanation:
The given terms are
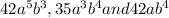
Now we have to prime factorize the each term.



Now we have to find the common factors in all the three terms.
The greatest common is nothing but the highest common divisor of all terms
The common factor is all the three terms are : 7, a, b*b*b
So the greatest common factor of given terms = 7*a*b*b*b =