Question

In ΔABC, which trigonometric ratio has the value a/c

A. Tan A
B. Cos A
C. Tan C
D. Cos C
E. Sin C

Answer 1

`\tan A`

Explanation:

From the diagram, side length
`a` is opposite to angle A and side length
`c` is adjacent to angle A.

Recall the mnemonics SOH CAH TOA.

We use TOA, because it involves opposite and adjacent.

`\tan A=(Opposite)/(Adjacent)`

`\tan A=(a)/(c)`

The correct choice is A.

Answer 2

Hello!

The answer is: A. Tan(A)

Why?

Since it's a right triangle, we must remember the following trigonometric identities:

`sin\alpha =(opposite)/(hypotenuse)\\\\cos\alpha =(adjacent)/(hypotenuse)\\\\tan\alpha=(opposite)/(adjacent)`

We are going to work with the tangent indentity, so:

If we are looking which a trigonometric ratio/relation which is equal to:

`(a)/(c)`

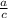
Also, from the image we can see that:

`opposite=a\\adjacent=c\\hypotenuse=b`

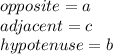
So, using the tangent identity, which is equal to:

`tan(A)=(opposite)/(adjacent)=(a)/(c)`

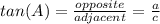
So, the correct option is A. Tan(A)

Have a nice day!