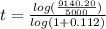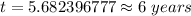Question

You plan to invest in securities pay more 11.2% compounded annually. if you invest $5000 today, how many years will it take for your investment to grow to $9,140.20

Answer 1

`t\approx6\hspace{3}years`

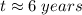
Step-by-step explanation:

When interest is compounded annually, we can use the following formula to calculate the amount in the account at the end of a given time period.:

`FV=PV(1+r)^t`

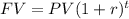
Where:

`FV=Future\hspace{3}value=9140.20\\PV=Present\hspace{3}value=5000\\r=Interest\hspace{3}rate=11.2\%=0.112\\t=Time`

Let's solve the previous equation for t:

Divide both sides by PV:

`(FV)/(PV) =(PV)/(PV) (1+r)^t\\\\(FV)/(PV) = (1+r)^t`

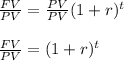
Take the natural logarithm of both sides:

`log((FV)/(PV)) = log( (1+r)^t)\\\\Use\hspace{3}the\hspace{3}identity\hspace{5}log(a^b)=b*log(a)\\\\log((FV)/(PV)) =t* log(1+r)\\\\Divide\hspace{3}both\hspace{3}sides\hspace{3}by\hspace{3}log(1+r)\\\\t=(log((FV)/(PV)))/(log(1+r))`

Replace the data provided by the problem:

`t=(log((9140.20)/(5000)))/(log(1+0.112))`

`t=5.682396777\approx 6\hspace{3}years`