Question

Adding two functions results in h(x) = –x + 9, while multiplying the same functions results in j(x) = –9x. Which statements describe f(x) and g(x), the original functions? Select two options. Both functions must be quadratic. Both functions must have a constant rate of change. Both functions must have a y-intercept of 0. The rate of change of either f(x) or g(x) must be 0. The y-intercepts of f(x) and g(x) must be opposites.

Answer 1

I think it is A and B. Tell me if im wrong

Answer 2

Both functions must have a constant rate of change.

The rate of change of either f(x) or g(x) must be 0.

Explanation:

We have that

`f(x)g(x)=-x+9\: \: \: \: (1)`

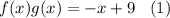
and

`f(x)g(x)=-9x\: \: \: \: (2)`

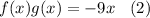
From the first equation we know that both f (x) and g (x) must be of order 1 or of order 0, since the maximum exponent of X is 1. This indicates that both functions must have a constant rate of change , since the derivative of a function of order 0 or of order 1 is a constant.

From equation 2 we know that both f (x) and g (x) are composed of a single term, since the multiplication of both results in a single term (-9x). In addition, we verify that one of the functions is of order 0 and the other is of order 1, since the result of the product is of order 1.

If f (x) or g (x) are of order 0, which means that they are composed of only one constant, the rate of change of any of the 2 functions is 0.