Question

solve the system of equations y = 2x - 4 y = x^2 - 4 A. (-3,5) and (3,5) B. (0,-4) and (2,0) C. (-1,-6) and (3,2) D. (0,4) and (2,1)

Answer 1

B. (0,-4) and (2,0)

Explanation:

The given system of equations is:

`y=2x-4`

`y=x^2-4`

Equate both equations and solve for x.

`x^2-4=2x-4`

`x^2-4-2x+4=0`

`x^2-2x=0`

Factor;

`x(x-2)=0`

`x=0,x-2=0`

`x=0,x=2`

When x=0, y=2(0)-4=-4

Hence (0,-4) is one solution

When x=2, y=2(2)-4=0

Hence (2,0) is another solution

The correct choice is B.

Answer 2

Hello!

The answer is: B. (0,-4) and (2,0)

Why?

We can solve the system of equations using the substitution method, meaning that we must substitute one equation into the other equation, resulting in a principal equation.

So,

We are given two equations:

`y=2x-4`

and,

`y=x^(2) -4`

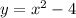
So, making the equation equals, we have that:

`2x-4=x^(2)-4\\x^(2)-2x-4+4=0\\x^(2)-2x=0\\x(x-2)=0\\`

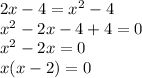
Finding where the function tends to 0 (roots), we have:

`x(x-2)=0\\x1=0\\x2=2`

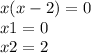
Then, substituting each value of "x" in the first equation, we will find the correct options:

Substituting "x" equal to 0 into the first equation, we have:

`y=2(0)-4=-4`

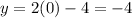
So, the point will be (0,-4)

Substituting "x" equal to 2 into the first equation, we have:

`y=2(2)-4=4-4=0`

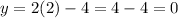
So, the point will be (2,0)

Therefore, the correct option is B. (0,-4) and (2,0)

Have a nice day!