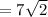Question

Can anybody help me on this?

Answer 1

Answer: second option.

Explanation:

You need to descompose the radicand 8 and the radicand 50 into their prime factors:

`8=2*2*2=2^2*2\\50=2*5*5=2*5^2`

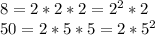
Then you can rewrite the expression:

`√(8)+√(50)`

`=√(2^2*2)+√(2*5^2)`

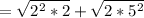
Since:

`√(a^2)=a`

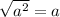
You can simplify the expression:

`=2√(2)+5√(2)`

As the indices and the radicands are the same, you can make the addition:

`=7√(2)`