Question

on a piece of paper, graph this system of equations. y = - x - 10 y = x^2 - 2x - 3 then determine which answer choice matches the graph you drew and identify the solution(s) to the system.

Answer 1

It's D

Explanation:

I got it right on Ap3x

Sorry if it's wrong for you.

Answer 2

Option D. No solution

Explanation:

We have the equation of a line:

`y = - x - 10`

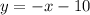
We find their cut points.

Cut point with the y axis. (x = 0)

`y = -(0) -10\\y = -10`

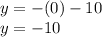
Cut point with the x axis. (y = 0)

`0 = -x -10\\x = -10`.

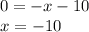The line cuts to the x-axis at
`x = -10` and cuts the y-axis at
`y = -10`

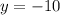
We have a parabola

`y = x ^ 2 - 2x - 3`

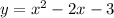
We can factor this quadratic equation by looking for 2 numbers that when multiplied give as result -3 and that when adding these numbers as a result -2. These numbers are -3 and 1.

Then the factors are:

`(x-3)(x + 1) = 0`

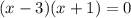
The zeros are 3 and -1. So the parabola cuts to the x axis at points 3 and -1.

Now we find the cut points with the y axis. (x = 0)

`y = (0-3)(0 + 1)\\y = -3.`

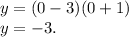
The parabola cuts to the axis y in y = -3.

Now we can graph the line and the parabola. Observe the attached image.

The system has no solution because the line and the parabola never intersect or touch each other. The answer is the option D