Question

What is the measure of angle A?

Enter your answer as a decimal in the box. Round only your final answer to the nearest hundredth.

°
triangle A B C with right angle A. A B equals 18. B C equals 80. A C equals 82.

Answer 1

Explanation:

You're answer to this question is 77.32, because I just took this quiz five seconds ago and this answer was shown

Answer 2

angle A is 77.32°

Explanation:

AB = c = 18

BC = a =82

AC = b = 80

To find angle A, we are going to use cosine formula;

a² = b² + c² - 2bc COS A

80² = 82² + 18² - 2(82)(18) COS A

6400 = 6724 + 324 - 2952 COSA

6400 = 7048 - 2952 COSA

Add 29852 COSA to both-side of the equation in other to take '29852 COSA' to the left-hand-side of the equation

6400 + 29852 COSA = 7048- 29852 COSA+29852 COSA

6400 + 29852 COSA = 7048

Subtract 6400 from both-side of the equation

6400 - 6400 + 29852 COSA = 7048 - 6400

29852 COSA = 648

Divide both-side of the equation by 29852

29852 COSA / 29852 = 648/29852

(On the left-hand side of the equation 29852 at the numerator will cancel-out 29852 at the denominator leaving us with just COSA while on the right-hand side of the equation 648 will be divided by 29852 )

COSA = 648 / 29852

COSA = 0.219512

But what we were ask to find is just angle A, to find angle A, take the
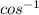`cos^(-1)` of both-side of the equation

`cos^(-1)` COSA =
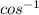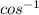`cos^(-1)` (0.219512)

A = 77.31963

A = 77.32° to the nearest hundredth

Therefore angle A is 77.32° to the nearest hundredth