Question

Work out the gradient of the straight line that passes through (2,6) and (6,12)

Answer 1

The gradient of the straight line that passes through (2, 6) and (6, 12) is
`m = (3)/(2)`.

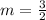Explanation:

Mathematically speaking, lines are represented by following first-order polynomials of the form:

`y = b + m\cdot x` (1)

Where:

`x` - Independent variable.

`y` - Dependent variable.

`m` - Slope.

`b` - Intercept.

The gradient of the function is represented by the first derivative of the function:

`y' = m`

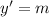
Then, we conclude that the gradient of the staight line is the slope. According to Euclidean Geometry, a line can be form after knowing the locations of two distinct points on plane. By definition of secant line, we calculate the slope:

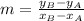`m = (y_(B)-y_(A))/(x_(B)-x_(A))` (2)

Where:

`x_(A)`,
`y_(A)` - Coordinates of point A.

`x_(B)`,
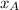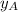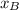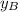`y_(B)` - Coordinates of point B.

If we know that
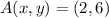`A(x,y) = (2,6)` and
`B(x,y) = (6,12)`, then the gradient of the straight line is:

`m = (12-6)/(6-2)`

`m = (6)/(4)`

`m = (3)/(2)`

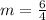
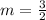
The gradient of the straight line that passes through (2, 6) and (6, 12) is
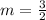`m = (3)/(2)`.