Question

Choose the function that shows the correct transformation of the quadratic function shifter eight units to the left and one unit down.

A. f(x)=(x-8)^2-1

B. f(x)=(x-8)^2+1

C. f(x)=(x+8)^2-1

D. f(x)=(x+8)^2+1

Answer 1

The function that shows the correct transformation of the quadratic function shifter eight units to the left and one unit down is:

Option C.
`f(x)=(x+8)^2-1`

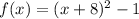
Explanation:

If we have a function f(x) then we can move its graph horizontally making the transformation
`y = f(x + c)`

Then if
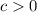`c> 0` the graph will move c units to the left.

If
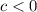`c <0` the graph will move c units to the right.

If we apply the transformation
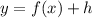`y = f(x) + h` then the graph of f(x) will move vertically h units.

If
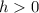`h> 0` the displacement will be h units up

If
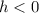`h <0` the displacement will be h units down.

In this problem we have the parent function
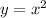`y = x ^ 2` and we want to move 8 units to the left and 1 unit to the bottom.

Then we apply the transformations described above with
`c = 8`.

`y = f(x + 8) = (x + 8) ^ 2`

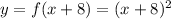
Now we must move the function 1 unit down, with
`h = -1`.

`y = f(x + 8) -1 = (x + 8) ^ 2 -1`

`f(x)= (x + 8) ^ 2 -1`

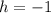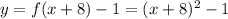
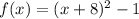
The answer is option C