Answer:
The correct answer is:
x = 4, solution is not extraneous
Explanation:
Extraneous solution--
It is the solution which is obtained from the equation i.e. by solving the equation but is not a valid solution to the equation.
True solution--
It is the solution which is obtained from the equation i.e. by solving the equation and is a valid solution to the equation.
Here we have the equation as:
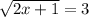
Now on squaring both the sides of the equation we have:
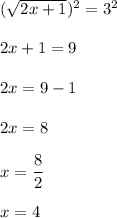
and the solution is a valid solution since the square root function is defined for this value of x.
Hence, the solution is not a extraneous solution i.e. it is a true solution to the equation.