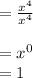Answer: Last option
Explanation:
You need to remember the Negative exponent rule:
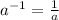
You also need to remember the Product ot poers property and the Quotient of powers property, which are:
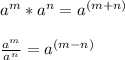
And:
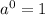
Therefore, you can rewrite the expression as following:
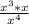
Applying the properties, you can simplify: