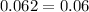Question

Identify the probability to the nearest hundredth that a point chosen randomly inside the rectangle is either in the circle or in the regular hexagon. HELP ASAP!!

Answer 1

`0.06`

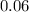
Explanation:

we know that

The probability of an event is the ratio of the size of the event space to the size of the sample space.

The size of the sample space is the total number of possible outcomes

The event space is the number of outcomes in the event you are interested in.

so

Let

x------> size of the event space

y-----> size of the sample space

so

`P=(x)/(y)`

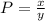
step 1

Find the probability that a point chosen randomly inside the rectangle is in the circle

Find the area of the rectangle

`A=26.2*13=340.6\ in^(2)`

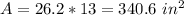
Find the area of the circle

`A=3.14*(2)^(2) =12.56\ in^(2)`

In this problem we have

`x=12.56\ in^(2)`

`y=340.6\ in^(2)`

substitute

`P=(12.56)/(340.6)=0.037`

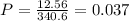
step 2

Find the probability that a point chosen randomly inside the rectangle is in the regular hexagon

Find the area of the regular hexagon

`A=6[(1)/(2) (1.8)^(2)sin(60)]=8.42\ in^(2)`

In this problem we have

`x=8.42\ in^(2)`

`y=340.6\ in^(2)`

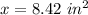
substitute

`P=(8.42)/(340.6)=0.025`

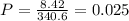
step 3

Find the probability that a point chosen randomly inside the rectangle is either in the circle or in the regular hexagon

Is the sum of the two probabilities

`0.037+0.025=0.062`

Round to the nearest hundredth

`0.062=0.06`