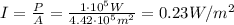Question

A radar for tracking aircraft broadcasts a 12 GHz microwave beam from a 2.0-m-diameter circular radar antenna. From a wave perspective, the antenna is a circular aperture through which the microwaves diffract Part A) What is the diameter of the radar beam at a distance of 30 km? Part B) If the antenna emits 100 kW of power, what is the average microwave intensity at 30 km? (In W/m^2)

Answer 1

A) 750 m

First of all, let's find the wavelength of the microwave. We have

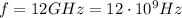`f=12GHz=12\cdot 10^9 Hz` is the frequency

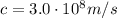`c=3.0\cdot 10^8 m/s` is the speed of light

So the wavelength of the beam is

`\lambda=(c)/(f)=(3\cdot 10^8 m/s)/(12\cdot 10^9 Hz)=0.025 m`

Now we can use the formula of the single-slit diffraction to find the radius of aperture of the beam:

`y=(m\lambda D)/(a)`

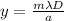
where

m = 1 since we are interested only in the central fringe

D = 30 km = 30,000 m

a = 2.0 m is the aperture of the antenna (which corresponds to the width of the slit)

Substituting, we find

`y=((1)(0.025 m)(30000 m))/(2.0 m)=375 m`

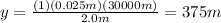
and so, the diameter is

`d=2y = 750 m`

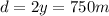
B) 0.23 W/m^2

First we calculate the area of the surface of the microwave at a distance of 30 km. Since the diameter of the circle is 750 m, the radius is

`r=(750 m)/(2)=375 m`

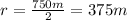
So the area is

`A=\pi r^2 = \pi (375 m)^2=4.42\cdot 10^5 m^2`

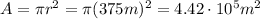
And since the power is

`P=100 kW = 1\cdot 10^5 W`

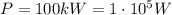
The average intensity is

`I=(P)/(A)=(1\cdot 10^5 W)/(4.42\cdot 10^5 m^2)=0.23 W/m^2`