Question

Determine the intervals on which the function is increasing, decreasing, and constant. An absolute value function is shown facing down with a vertex of -1,0.

Answer 1

(-infinity, 0)

Explanation:

Answer 2

Increasing on:
`x\:<\:-1`

Decreasing on:
`x\:>\:-1`

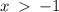
Constant at : x=-1

Explanation:

The given absolute value function is
`f(x)=|x+1|`.

A function is said to be increasing if for all
`x_1\:>\:x_0`,
`f(x_1)\:>\:f(x_0)`

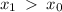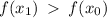
From the graph, we can observe that the graph has a positive slope for all x-values less than -1. This implies that the interval of increase is
`x\:<\:-1` or
`(-\infty,-1)`

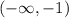
We can also observe that, the slope of this function is negative on the interval:
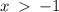`x\:>\:-1` or
`(-1,\infty)`.

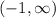At x=-1, the function is neither increasing nor decreasing. We say the function is constant at x=-1