Question

The length of a rectangle is 3 in more than twice it’s width, and it’s area is 65 sq in. What is it’s width?

Answer 1

The width is 5in.

Explanation:

Let the width of the rectangle be
`w\:in.`.

The length of a rectangle is 3 in more than twice it’s width, so we write the equation;

`l=(2w+3)in`

The area of the rectangle is given by;

`Area=lw`

it was given that the area is 65 sq in.

This implies that;

`65=(2w+3)w`

Expand the brackets

`65=2w^2+3w`

`2w^2+3w-65=0`

Factor

`(2w+13)(w-5)=0`

`(2w+13)=0,(w-5)=0`

`w=-(13)/(2),w=5`

Discard the negative value.

Hence
`w=5in.`

Answer 2

Answer: 5 inches.

Explanation:

The formula for calculate the area of a rectangle is:

`A=w*l`

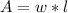
Where l is the length and w is the width.

If the length of a rectangle is 3 inches more than twice it’s width, then:

`l=2w+3`

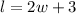
Substitute
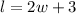`l=2w+3` and the area into the formula and solve for the width:

`65=(2w+3)w\\65=2w^2+3w\\0=2w^2+3w-65`

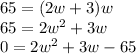
Use the quadratic formula:

`w=(-b\±√(b^2-4ac))/(2a)\\\\w=(-3\±√(3^2-4(2)(-65)))/(2(2))\\\\w=5\\w=-6.5`

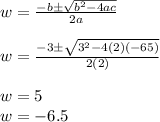
Choose the positive value.

Therefore, the width is: 5 inches.