Question

The central star of a planetary nebula emits ultraviolet light with wavelength 104nm. This light passes through a diffraction grating with 5000 slits per mm. What is the first-order diffraction angle?

Answer 1

Answer: 31.33 degrees

Step-by-step explanation:

The diffraction angles
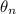`\theta_(n)` when we have a slit divided into
`n` parts are obtained by the following equation:

`dsin\theta_(n)=n\lambda` (1)

Where:

`d` is the width of the slit

`\lambda` is the wavelength of the light

`n` is an integer different from zero.

Now, the first-order diffraction angle is given when
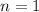`n=1`, hence equation (1) becomes:

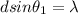`dsin\theta_(1)=\lambda` (2)

Now we have to find the value of
`\theta_(1)`:

`sin\theta_(1)=(\lambda)/(d)`

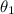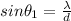
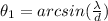`\theta_(1)=arcsin((\lambda)/(d))` (3)

We know:

`\lambda=104nm=104(10)^(-9)m`

In addition we are told the diffraction grating has 5000 slits per mm, this means:

`d=(1mm)/(5000)=(1(10)^(-3)m)/(5000)`

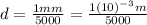
Substituting the known values in (3):

`\theta_(1)=arcsin((104(10)^(-9)m)/((1(10)^(-3)m)/(5000)))`

`\theta_(1)=arcsin(0.52)`

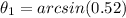
Finally:

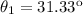`\theta_(1)=31.33\º` >>>This is the first-order diffraction angle