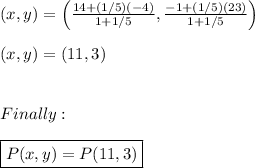Answer:
D. (11,3)
Explanation:
First of all, let's plot each point as indicated in figure below. To find the point
 that divide a segment with endpoints
that divide a segment with endpoints
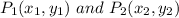 and a ratio:
and a ratio:
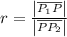
We must use the formula:
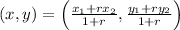
To find the ratio, we know that:

because
 is 1/6 of the way from
is 1/6 of the way from
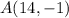 to
to
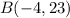
So the other part of the segment is:
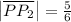
Therefore, the ratio can be found as:
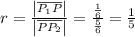
From here, we can calculate the point we are looking for: